玩计算器的发现
大家都玩过计算器吧, 不知注意到没有.
输入任意数, 然后不断按最后总会输出
.
什么, 你说明明记得是:? 哦, 因为你用了角度制.
这一系列操作等价于求解方程, 角度制下就是
.
当然对于现在的你来说求数值解没啥意思了, 要求就求解析解是吧.
不过这两个方程其实是一样的, 我们先变个形:
也就是说:
于是我们现在只要解决这一个方程了.
最早研究这个问题的是天文学家, 毕竟那时候也没什么计算器给你玩, 一切要从实际出发...
开普勒方程
你可能听说过, 三体问题很困难, 直到一百多年前的庞加莱时代才被搞定.
而二体问题则简单的多, 400年前开普勒时代就研究的差不多了.
你至少知道这个成果, 两个天体以一个为交点, 另一个必定在圆锥曲线上运动.
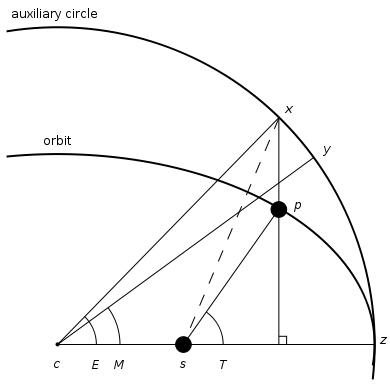
一般天体遵循椭圆轨道, 如图椭圆是实际运行的轨道, 与椭圆相切的是一个以半长轴为半径的辅助圆.
在一定的时间内, 椭圆轨道上的质点运行到了
点, 而辅助圆上的假想质点运行到了
点.
- 椭圆轨道上所转过的角度
被称为真近点角(True Anomaly)
- 辅助圆轨道上假想质点所转过的角度
被称为平近点角(Mean Anomaly)
- 将椭圆上的质点向上作延长线,交辅助圆于
点所形成的角
被称为偏近点角(Eccentric Anomaly)
天文学家发现, 它们满足如下关系式:
Kepler Equation:
抛物线就是的特殊情况, 双曲线有所不同.
Hyperbolic Kepler Equation:
但从数学上讲, 这个式子其实就是:
也就是说不考虑物理意义其实是一样的.
开普勒方程的解析解
有了方程当然接下来就是求解了咯, 古代计算力比较值钱, 毕竟没有计算机, 所以大家对解析解都有一种病态的追求.
怎么着推一天公式要比算一整天的牛顿迭代有趣吧?
作一下等价性检验:
In [] = FindRoot[x==Cos@x,{x,0}] x-Pi/2/.FindRoot[Pi/2==x-Sin@x,{x,1}] FindRoot[x==Cos[Pi x/180],{x,0}] 180x/Pi-90/.FindRoot[Pi/2==x-Pi Sin@x/180,{x,1}]Out[] = 0.7390851332151605` {x -> 0.7390851332151607`} 0.9998477415310987` {x -> 0.9998477415310881`} 拉格朗日反演
不能分离但
, 展开
,然后直接用级数反演即可.
Mathematica 可以很方便的执行级数反演.
Series[M- Sin[M], {M, 0, 10}]//InverseSeriesSeries[M-e Sin[M], {M, 0, 10}]//InverseSeries 早期解这个方程使用了关于离心率的麦克劳林展开.
这不是个整函数, 所以引入了所谓的拉普拉斯极限.
超出收敛域的部分级数失效, 级数反演则很好的解决了这个问题.
贝塞尔函数解
当然无穷级数不利于计算, 能否使用微积分表达是我们接下来的探索重点.
我们来考虑函数方程:
我们假设它可以展开为傅里叶级数, 分析原函数方程性态可以期望这是个正弦级数.
那么系数可以表达为:
我们来尝试计算, 嗯? 没思路怎么办...
无脑分部积分展开到能搞定为止呗.
而这正好是贝塞尔函数的定义式之一:
Bessel Function of the First Kind:
于是原式可以写成
赫维茨-勒奇超越函数解
上有个用反三角函数和三角函数表示的解析解, 这个解比较有难度.
特殊函数论中将以下级数称为赫维茨-勒奇超越函数(Lerch Transcendent Function)
我们从上面的贝塞尔函数解开始, 还原掉贝塞尔函数:
然后交换积分求和顺序.
里面的部分圈起来叫, 用欧拉公式展开.
其中:
可以发现其实都是的结构.
我们引入多对数函数:
也就是说:
用这个函数化简等式:
同样的整理一下:
可以合并成两组, 然后再次展开, 运算量有点大.
化简的时候注意恒等式:.
注意到第二部分:
最后代回去大功告成!
代入数据就得到了 Stack Exchange 一样的结果.
我对这种写法感到很不爽.
这个当然不能直接抵消, 由于, 我们作复展开.
严格来说这两者不是完全相等的, 因为这样一来消掉了奇点.
不过积分的时候完全可以划等号, 因为区间开闭完全不影响积分值.
综上所述, 最后代入值, 我们得到了:
(*真男人从不回头看数值验证*)(2 + I Integrate[Log[-I/E^(I*(t - Sin[t]))], {t, 0, Pi}])/(2*Pi)//N(Pi + 90I Integrate[Log[(-I)*E^((-I)*t + (1/180)*I*Pi*Sin[t])], {t, 0, Pi}])/Pi^2//N> 0.7390851332151609` > 0.9998477415310951` 只有娘们才喜欢用特殊函数
最后一个是上的, 这个答案就非常魔幻了,它和上面两个方法不是一个系列的, 和第一个方法有关.
暴力求解拉格朗日反演的解析形式, 场面非常的少儿不宜...
我一时半会儿也没看懂,详情看参考书目(3).
从这个结果上也能看出这个方法有多残暴...
(*怎么可以这么暴力的说*)\[Pi]/2 Exp[NIntegrate[1/(\[Pi] x) ArcTan[((\[Pi] x+2)Log[(Sqrt[1-x^2]+1)/x]x)/(x^2Log[(Sqrt[1-x^2]+1)/x]^2-\[Pi] x-1)],{x,0,1},WorkingPrecision->50]]ArcCot[1+1/(2\[Pi] ) NIntegrate[Log[((1-x^2)Pi^2+4(Sqrt[1-x^2]ArcTanh[x]+x)^2)/((1-x^2)Pi^2+4(Sqrt[1-x^2]ArcTanh[x]-x)^2)],{x,0,1},WorkingPrecision->50]]> 0.73908513321516064165531208767387340401341175890075746496567242428255184768807`50.12267193056545> 0.73908513321516064165531208767387340401341175890075746496567993239614795659229`51.22422170141253 参考书目
- On Taylor series and Kapteyn series of the first and second type
- Kepler's equation, radiation problems and Meissel's expansion
- An exact analytical solution of Kepler's Equation
玩计算器的发现
大家都玩过计算器吧, 不知注意到没有.输入任意数, 然后不断按\mathtt{cos\ ANS}最后总会输出0.739085.
什么, 你说明明记得是:0.999847? 哦, 因为你用了角度制.
这一系列操作等价于求解方程x=\cos x, 角度制下就是x=\cos x°=\cos\dfrac{\pi x}{180}.
当然对于现在的你来说求数值解没啥意思了, 要求就求解析解是吧.
不过这两个方程其实是一样的, 我们先变个形:
\begin{aligned} x=\cos x\;\Longrightarrow& x-\frac{\pi}{2}=\cos \left(x-\frac{\pi}{2}\right)&=\sin x\\ x=\cos x°\Longrightarrow& \frac{180 x}{\pi }-90=\cos \left(\frac{ \pi}{180} \left(\frac{180 x}{\pi }-90\right)\right)&=\sin x \end{aligned}
也就是说:
于是我们现在只要解决Ax-B=\sin(x)这一个方程了.
最早研究这个问题的是天文学家, 毕竟那时候也没什么计算器给你玩, 一切要从实际出发...
开普勒方程
你可能听说过, 三体问题很困难, 直到一百多年前的庞加莱时代才被搞定.而二体问题则简单的多, 400年前开普勒时代就研究的差不多了.
你至少知道这个成果, 两个天体以一个为交点, 另一个必定在圆锥曲线上运动.
一般天体遵循椭圆轨道, 如图椭圆是实际运行的轨道, 与椭圆相切的是一个以半长轴为半径的辅助圆.在一定的时间t内, 椭圆轨道上的质点运行到了p点, 而辅助圆上的假想质点运行到了y点.
椭圆轨道上所转过的角度\angle T被称为真近点角(True Anomaly)
辅助圆轨道上假想质点所转过的角度\angle M被称为平近点角(Mean Anomaly)将椭圆上的质点向上作延长线,交辅助圆于x点所形成的角\angle E被称为偏近点角(Eccentric Anomaly)天文学家发现, 它们满足如下关系式:Kepler Equation:M= E-\epsilon \sin(E)
抛物线就是\epsilon=1的特殊情况, 双曲线有所不同.Hyperbolic Kepler Equation:M = \epsilon \sinh H - H \quad\mathrm{where}\quad H=iE
但从数学上讲, 这个式子其实就是:M = i \left( E - \epsilon \sin E \right)
也就是说不考虑物理意义其实是一样的.
开普勒方程的解析解
有了方程当然接下来就是求解了咯, 古代计算力比较值钱, 毕竟没有计算机, 所以大家对解析解都有一种病态的追求.怎么着推一天公式要比算一整天的牛顿迭代有趣吧?
\left\{\begin{aligned} \frac{\pi}{2}&=x-\sin x\\ \frac{\pi}{2}&=x-\frac{\pi}{180}\sin x \end{aligned}\right.
作一下等价性检验:
In [] = FindRoot[x==Cos@x,{x,0}]
x-Pi/2/.FindRoot[Pi/2==x-Sin@x,{x,1}] FindRoot[x==Cos[Pi x/180],{x,0}] 180x/Pi-90/.FindRoot[Pi/2==x-Pi Sin@x/180,{x,1}]Out[] = 0.7390851332151605`
{x -> 0.7390851332151607`} 0.9998477415310987` {x -> 0.9998477415310881`} 拉格朗日反演E不能分离但M, 展开M(E),然后直接用级数反演即可.M(E) = (1-\epsilon)E+\epsilon\sum _{n=1}^{\infty } \frac{(-1)^n}{(2 n+1)!}E^{2 n+1}
\bigstar E(M)= \begin{cases} \displaystyle \sum _{n=1}^{\infty }\bigg(\lim_{\theta \to 0^{+}}\!{\frac {\mathrm {d} ^{\,n-1}}{\mathrm {d} \theta ^{\,n-1}}}{\bigg (}{\frac {\theta }{\sqrt[{3}]{\theta -\sin(\theta )}}}{\bigg )}^{\!\!\!n}{\bigg )}{\frac {M^{\frac{n}{3}}}{n!}}&\epsilon=1\\ \displaystyle \sum_{n=1}^{\infty }\bigg(\lim_{\theta \to 0^{+}}{\frac {\mathrm {d} ^{\,n-1}}{\mathrm {d} \theta ^{\,n-1}}}{\Big (}{\frac {\theta }{\theta -\epsilon\sin(\theta )}}{\Big )}^{\!n}{\bigg )}{\frac {M^{n}}{n!}}&\epsilon\neq 1 \end{cases}
Mathematica 可以很方便的执行级数反演.
Series[M- Sin[M], {M, 0, 10}]//InverseSeries
Series[M-e Sin[M], {M, 0, 10}]//InverseSeries早期解这个方程使用了关于离心率\epsilon的麦克劳林展开.E(M)=M+\sum_{n=1}^\infty a_n \epsilon^n;\ \epsilon\leq\mathrm{L}
这不是个整函数, 所以引入了所谓的拉普拉斯极限.
L=\max_{x\in\mathbb{R}}\frac{x}{\cosh (x)}\approx0.662743
超出收敛域的部分级数失效, 级数反演则很好的解决了这个问题.
贝塞尔函数解
当然无穷级数不利于计算, 能否使用微积分表达是我们接下来的探索重点.我们来考虑函数方程:g (M) = E (M) - M
我们假设它可以展开为傅里叶级数, 分析原函数方程性态可以期望这是个正弦级数.
g (M) = \sum_{n = 1}^{\infty}a_n\sin (n M)
那么系数可以表达为:
a_n = \frac {2}{\pi}\int_0^\pi g(M) \sin(nM)\,\mathrm{d}M
我们来尝试计算, 嗯? 没思路怎么办...
无脑分部积分展开到能搞定为止呗.
\begin{aligned} a_n&=\frac{2}{\pi n}\int_0^\pi \cos(nM)\,\mathrm{d}g(M) -\frac{2}{\pi}\left[g(M)\frac{\cos(nM)}{n}\right]_0^\pi\\ &=\frac{2}{\pi n}\int_0^\pi \cos(nM)\,\mathrm{d}(E-M)\\ &=\frac{2}{\pi n}\int_0^\pi \cos[n(E-\epsilon\sin E)]\,\mathrm{d}E -\frac{2}{\pi n}\int_0^\pi \cos(nM)\,\mathrm{d}M\\ &=\frac{2}{\pi n}\int_0^\pi \cos(nE-n\epsilon\sin E)\,\mathrm{d}E \end{aligned}
而这正好是贝塞尔函数的定义式之一:
Bessel Function of the First Kind:J_n(z)=\frac{1}{\pi}\int_0^\pi \cos(n θ-z \sin θ)\,\mathrm{d}θ\ ;n\in \mathbb{Z}
于是原式可以写成\bigstar E(M)=M+\sum _{n=1}^{\infty } \frac{2}{n}J_n(n \epsilon )\sin(nM)
赫维茨-勒奇超越函数解
Stack Exchange上有个用反三角函数和三角函数表示的解析解, 这个解比较有难度.\mathcal{D}=\frac1\pi \int_0^{\pi } \arctan\left(\tan \left(\frac{t-\sin t+\frac{\pi }{2}}2\right)\right) \,\mathrm{d}t+\frac{1}{\pi }
特殊函数论中将以下级数称为赫维茨-勒奇超越函数(Lerch Transcendent Function)\Phi (z,t,h):=\sum _{n=0}^{\infty } \frac{z^n}{(h+n)^t}
我们从上面的贝塞尔函数解开始, 还原掉贝塞尔函数:
E=M+\sum _{n=1}^{\infty } \frac{2}{n}\left[\frac{1}{\pi}\int_0^\pi \cos(n θ-n\epsilon \sin θ)\,\mathrm{d}θ\right]\sin(nM)
然后交换积分求和顺序.
E=M+\frac{2}{\pi}\int_0^\pi\left[\sum _{n=1}^{\infty } \frac{\sin(nM)}{n} \cos(n θ-n\epsilon \sin θ)\right]\,\mathrm{d}θ
里面的部分圈起来叫F(M), 用欧拉公式展开.\begin{aligned} F(M)=&\frac{\sin(nM)}{n} \cos(n θ-n\epsilon \sin θ)\\ =&\frac{i}{4 n}\left(e^{-i M n}-e^{i M n}\right) \left(e^{-i (\theta n-n \epsilon \sin (\theta ))}+e^{i (\theta n-n \epsilon \sin (\theta ))}\right)\\ =&\frac{i}{4 n}\left(e_1+e_2+e_3+e_4\right) \end{aligned}
其中:
\begin{cases} e_1=+\exp(-i M n+i \theta n-i n \epsilon \sin (\theta ))\\ e_2=-\exp(i M n+i \theta n-i n \epsilon \sin (\theta ))\\ e_3=+\exp(-i M n-i \theta n+i n \epsilon \sin (\theta ))\\ e_4=-\exp(i M n-i \theta n+i n \epsilon \sin (\theta ))\\ \end{cases}
可以发现其实都是e^{n\alpha}的结构.
我们引入多对数函数:
\mathrm{Li}_s(z) := z\Phi (z,s,1)=\sum _{n=1}^{\infty } \frac{z^n}{n^s}
也就是说:
\sum _{n=1}^{\infty } \frac{e^{a n}}{n}=\text{Li}_1\left(e^a\right)=i\arg (1-e^a)-\ln |1-e^a|
用这个函数化简等式:
\begin{aligned} E=&M+\frac{2}{\pi}\int_0^\pi\left[\sum _{n=1}^{\infty } \frac{i}{4 n}\left(e_1+e_2+e_3+e_4\right)\right]\,\mathrm{d}θ\\ =&M+\frac{i}{2\pi}\int_0^\pi\left[\text{Li}_1(e^{a_1})+\text{Li}_1(e^{a_2})+\text{Li}_1(e^{a_3})+\text{Li}_1(e^{a_4})\right]\,\mathrm{d}θ \end{aligned}
同样的整理一下:
\begin{cases} a_1=+i (\theta -M-\epsilon \sin (\theta ))\\ a_2=+i (\theta +M-\epsilon \sin (\theta ))\\ a_3=-i (\theta +M-\epsilon \sin (\theta ))\\ a_4=-i (\theta -M-\epsilon \sin (\theta ))\\ \end{cases}
可以合并成两组, 然后再次展开, 运算量有点大.
化简的时候注意恒等式:\arg(e^{ix})=\arctan(\tan (x)).
\begin{aligned} \sum \text{Li}_1(e^{a}) =&\frac{2}{i}\arctan\tan \left(\frac{\theta -M-\epsilon \sin (\theta )+\pi}{2} \right)\\ +&\frac{2}{i}\arctan\tan \left(\frac{-\theta -M+\epsilon \sin (\theta )+\pi}{2}\right) \end{aligned}
注意到第二部分:
\int_0^{\pi } \arctan\cot \left(\frac{1}{2} (\theta +M-\epsilon \sin (\theta ))\right) \, \mathrm{d}\theta =\epsilon+\frac{1}{4} \left( +\pi ^2-2 \pi M\right)
最后代回去大功告成!
\begin{aligned} \bigstar E=&M+\frac{i}{2\pi}\int_0^\pi\sum \text{Li}_1(e^{a})\,\mathrm{d}θ\\ =&\frac{1}{4} (2 M+\pi )+\frac{\epsilon }{\pi }+\frac{1}{\pi }\int_0^\pi\arctan\tan \left(\frac{\theta -M-\epsilon \sin (\theta )+\pi}{2} \right)\mathrm{d}\theta \end{aligned}
代入数据就得到了 Stack Exchange 一样的结果.
我对\arctan(\tan (x))这种写法感到很不爽.
这个当然不能直接抵消, 由于\arctan(\tan (x)) \neq x, 我们作复展开.
\begin{aligned} \arctan(\tan (x)) &=\frac{1}{2} i \log \left(1+\frac{e^{-i x}-e^{i x}}{e^{-i x}+e^{i x}}\right)-\frac{1}{2} i \log \left(1-\frac{e^{-i x}-e^{i x}}{e^{-i x}+e^{i x}}\right)\\ &=\frac{i}{2}\log \left(\frac{2}{1+e^{2 i x}}\biggl/\frac{2 e^{2 i x}}{1+e^{2 i x}}\right)\\ &=\frac{i}{2}\log (e^{-2 i x}) \end{aligned}
严格来说这两者不是完全相等的, 因为这样一来消掉了奇点.
不过积分的时候完全可以划等号, 因为区间开闭完全不影响积分值.
\bigstar E=\frac{1}{4} (2 M+\pi )+\frac{\epsilon }{\pi }+\frac{i}{2\pi }\int_0^\pi \log \left(-e^{i (M+\epsilon \sin\theta-\theta)}\right)\mathrm{d}\theta
综上所述, 最后代入值, 我们得到了:
\begin{aligned} \mathcal{D}_{\;}=&\frac{1}{\pi }\left[1+\frac{i}{2}\int_0^{\pi}\log \left(-i e^{i (\sin t-t)}\right)\;\mathrm{d}t\right]\\ \mathcal{D}_°=&\frac{1}{\pi }\left[1+\frac{90i}{\pi}\int_0^{\pi}\log \left(-i e^{i (\pi\sin t/180-t)}\right)\;\mathrm{d}t\right] \end{aligned}
(*真男人从不回头看数值验证*)
(2 + I Integrate[Log[-I/E^(I*(t - Sin[t]))], {t, 0, Pi}])/(2*Pi)//N(Pi + 90I Integrate[Log[(-I)*E^((-I)*t + (1/180)*I*Pi*Sin[t])], {t, 0, Pi}])/Pi^2//N> 0.7390851332151609`
> 0.9998477415310951` 只有娘们才喜欢用特殊函数最后一个是百度贴吧上的, 这个答案就非常魔幻了,它和上面两个方法不是一个系列的, 和第一个方法有关.暴力求解拉格朗日反演的解析形式, 场面非常的少儿不宜...
我一时半会儿也没看懂,详情看参考书目(3).
\begin{aligned} \mathcal{D}=&\frac{1}{2} \pi \exp \left(\int_0^1 {\frac{1}{\pi x}\arctan\left(\frac{x \log \left(\frac{\sqrt{1-x^2}+1}{x}\right)(\pi x+2) }{x^2 \log ^2\left(\frac{\sqrt{1-x^2}+1}{x}\right)-\pi x-1}\right) \, \mathrm{d}x}\right)\\ =&\mathrm{arccot}\left(1+\frac{1}{2 \pi }\int_0^1{ \log \left(\frac{\pi ^2 \left(1-x^2\right)+4 \left(\sqrt{1-x^2} \mathrm{arctanh}(x)+x\right)^2}{\pi ^2 \left(1-x^2\right)+4 \left(\sqrt{1-x^2} \mathrm{arctanh}(x)-x\right)^2}\right) \, \mathrm{d}x}\right) \end{aligned}
从这个结果上也能看出这个方法有多残暴...
(*怎么可以这么暴力的说*)
\[Pi]/2 Exp[NIntegrate[1/(\[Pi] x) ArcTan[((\[Pi] x+2)Log[(Sqrt[1-x^2]+1)/x]x)/(x^2Log[(Sqrt[1-x^2]+1)/x]^2-\[Pi] x-1)],{x,0,1},WorkingPrecision->50]]ArcCot[1+1/(2\[Pi] ) NIntegrate[Log[((1-x^2)Pi^2+4(Sqrt[1-x^2]ArcTanh[x]+x)^2)/((1-x^2)Pi^2+4(Sqrt[1-x^2]ArcTanh[x]-x)^2)],{x,0,1},WorkingPrecision->50]]> 0.73908513321516064165531208767387340401341175890075746496567242428255184768807`50.12267193056545
> 0.73908513321516064165531208767387340401341175890075746496567993239614795659229`51.22422170141253参考书目On Taylor series and Kapteyn series of the first and second typeKepler's equation, radiation problems and Meissel's expansionAn exact analytical solution of Kepler's Equation
我很早就一直想写一篇文章,跟大家聊一聊:
1. 首先我们要复习一下三角函数。
对于任意的角 x, 我们有 {\sin^2 x}+\cos^2x=1,这跟勾股定理是一回事。
接下来是一个重要的公式,建议读者通过画图理解

然后通过画出三角函数图像的方式,我们还可以轻易验证如下两条公式
2. 现在我们可以开始证明了。
(该证明取自美国数学月刊2002年2月第109期 pp. 196-200 作者系Josef Hofbauer。)
2.1
由于 \sin(2x) = 2 \sin x \cos x,所以
根据定义可知
现在,利用恒等式 \sin(π-x)=\sin x,可得
2.2
有读者可能要问,为什么要像刚才那样做,其实原因马上就很清楚了,目的只有一个:让所有 \sin()里的值都是锐角。
因为对于锐角x,我们有 \sin x < x < \tan x

(各位读者请注意,刚才这三个不等关系(3)(4)(5)可能需要花时间仔细读懂。尤其是(3),是全文中最难理解的一步,希望读者能耐心地读懂:如何可以从之前的公式(1)(2)推导出(3)?)
2.3
通过观察,我们可以发现,之前在(**)中,我们只用到
则有
2.4
现在我们离结论只有一步之遥,
令
证明完毕!
怎么样,好玩吧,数学永远是这样,用最巧妙的逻辑链条构造最美丽的证明。
只要有一点点好奇心,和足够的耐心,人人都可以享受数学的乐趣。祝大家暑假愉快。
贾博名
2014年6月20日 于 美国俄亥俄州哥伦布市 (最新一次更新于2016年6月19日,再次感谢孙豪同学对本文初稿的认真阅读,并指出了多处笔误,现已更正。)